[Algorithm] 동적 계획법(DP)
Updated:
1. 개요
동적 계획법은 영어로 DP(Dynamic Programming)라고 부른다. 큰 문제를 작은 문제로 나눠서 풀기 위한 알고리즘으로 연산의 결과를 캐시에 저장하여 재활용 함으로써 중복되는 연산을 단 한 번씩만 수행한다. 따라서 프로그램의 실행 속도를 향상시킬 수 있다.
2. 동적 계획법의 조건
동적 계획법은 Overlapping Subproblem과 Optimal Substructure라는 두 가지 조건을 모두 만족해야 한다.
2-1. Overlapping Subproblem
문제를 작은 문제로 쪼갤 수 있고, 원래의 문제와 쪼갠 문제를 같은 방법으로 풀 수 있어야 한다.

2-2. Optimal Substructure
문제의 정답을 작은 문제의 정답에서 구할 수 있어야 하고, 한 문제의 정답은 크기에 상관없이 일정해야 한다.

3. 메모이제이션(Memoization)
동적 계획법은 연산의 결과를 캐시에 저장해 놓고, 필요할 때 재활용하므로 중복되는 연산을 단 한번씩만 수행할 수 있다. 연산의 결과를 보통은 배열에 저장하는데, 이를 메모이제이션(Memoization)이라고 한다.
3-1. 일반적인 피보나치 수
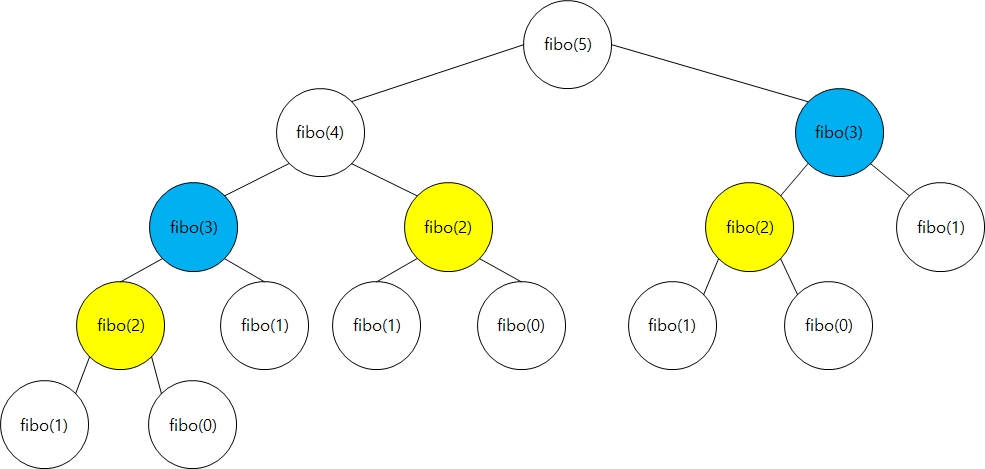
1
2
3
4
int fibo(int n) {
if (n <= 1) return n;
return fibo(n - 1) + fibo(n - 2);
}
3-2. 메모이제이션을 이용한 피보나치 수
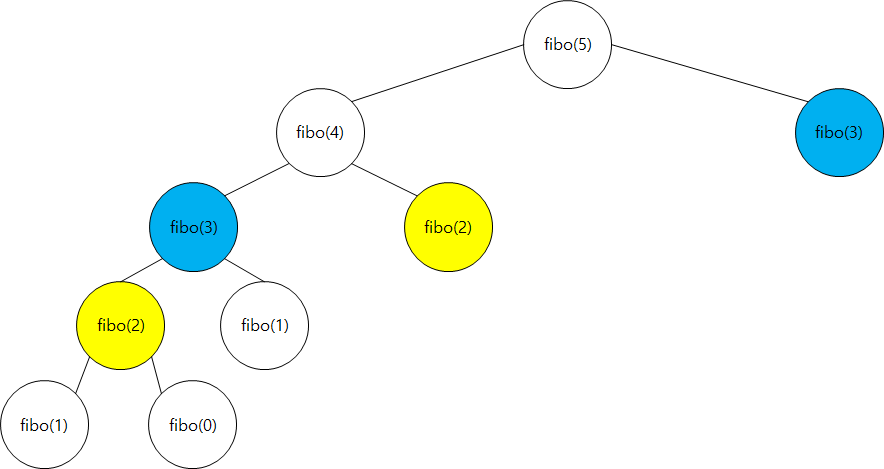
1
2
3
4
5
6
7
int d[10];
int fibo(int n) {
if (n <= 1) return n;
if (d[n] > 0) return d[n];
return d[n] = fibo(n - 1) + fibo(n - 2);
}
4. 구현 방법
동적 계획법의 구현은 Top-Down, Bottom-Up 두 가지 방법이 있다.
4-1. Top-Down
큰 문제를 작은 문제로 나눠서 푸는 방법으로, 재귀로 구현한다.
1
2
3
4
5
6
7
int d[10];
int fibo(int n) {
if (n <= 1) return n;
if (d[n] > 0) return d[n];
return d[n] = fibo(n - 1) + fibo(n - 2);
}
4-2. Bottom-Up
작은 문제부터 차례대로 푸는 방법으로, 반복문으로 구현한다.
1
2
3
4
5
6
7
8
9
int d[10];
int fibo(int n) {
d[0] = 0; d[1] = 1;
for (int i = 2; i <= n; ++i) {
d[i] = d[i - 1] + d[i - 2];
}
return d[n];
}

Leave a comment