[Algorithm] 유클리드 호제법(Euclidean Algorithm)

1. 개요

최대공약수를 구할 때 유클리드 호제법(Euclidean Algorithm)을 이용하면, 모든 정수로 나눠가면 계산할 때 보다 빠른 시간에 최대공약수를 구할 수 있다. 이번에는 유클리드 호제법(Euclidean Algorithm)을 이용하여 최대공약수를 구하는 방법에 대해 알아보도록 하자.

2. 최대공약수(GCD)

두 수의 공약수 중 가장 큰 수를 최대공약수라고 한다.

EX) 9와 18의 최대공약수

• 9의 약수 = 1, 3, 9

• 18의 약수 = 1, 2, 3, 6, 9, 18

• 9와 18의 공약수 = 1, 3, 9

∴ 9와 18의 최대공약수 = 9

3. 최소공배수(LCM)

두 수의 공배수 중 가장 작은 수를 최소공배수라고 한다.

EX) 9와 18의 최소공배수

• 9의 배수 = 9, 18, 27, …

• 18의 약수 = 18, 36, 54, …

• 9와 18의 공배수 = 18, 36, 54, …

∴ 9와 18의 최소공배수 = 18

두 수를 A, B라고 할 때, 아래 공식을 통해 최소공배수를 구할 수 있다.

LCM * GCD = A * B

LCM = A * B / GCD

4. 유클리드 호제법

A를 B로 나눈 나머지를 R이라고 할 때, GCD(B, R)을 계산하며 R이 0이 되었을 때 B의 값이 최대공약수가 된다.

EX) 9와 18의 최대공약수

• GCD(9, 18)

• GCD(18, 9)

• GCD(9, 0)

∴ 9와 18의 최대공약수 = 9

5. 구현 코드

유클리드 호제법은 재귀나 반복문을 사용하여 구현할 수 있다.

5-1. C++

5-1-1. 재귀함수 사용

[소스 코드]

https://github.com/dev-aiden/problem-solving/blob/main/algorithm/euclidean.cpp

#include <iostream>

using namespace std;

int gcd(int a, int b) {
    if (b == 0) return a;
    else return gcd(b, a % b);
}

int lcm(int a, int b) {
    return a * b / gcd(a, b);
}

int main(void) {
    ios_base::sync_with_stdio(false);
    int a, b; cin >> a >> b;
    cout << gcd(a, b) << "\n";
    cout << lcm(a, b) << "\n";
    return 0;
}

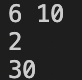
[실행 결과]

5-1-2. 반복문 사용

[소스 코드]

https://github.com/dev-aiden/problem-solving/blob/main/algorithm/euclidean2.cpp

#include <iostream>

using namespace std;

int gcd(int a, int b) {
    while (b != 0) {
        int r = a % b;
        a = b;
        b = r;
    }
    return a;
}

int lcm(int a, int b) {
    return a * b / gcd(a, b);
}

int main(void) {
    ios_base::sync_with_stdio(false);
    int a, b; cin >> a >> b;
    cout << gcd(a, b) << "\n";
    cout << lcm(a, b) << "\n";
    return 0;
}

[실행 결과]

5-2. JAVA

5-2-1. 재귀함수 사용

[소스 코드]

https://github.com/dev-aiden/problem-solving/blob/main/algorithm/euclidean.java

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Euclidean {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int a = Integer.parseInt(st.nextToken());
        int b = Integer.parseInt(st.nextToken());
        System.out.println(gcd(a, b));
        System.out.println(lcm(a, b));
    }

    public static int gcd(int a, int b) {
        if (b == 0) return a;
        else return gcd(b, a % b);
    }

    public static int lcm(int a, int b) {
        return a * b / gcd(a, b);
    }
}

[실행 결과]

5-2-2. 반복문 사용

[소스 코드]

https://github.com/dev-aiden/problem-solving/blob/main/algorithm/euclidean2.java

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int a = Integer.parseInt(st.nextToken());
        int b = Integer.parseInt(st.nextToken());
        System.out.println(gcd(a, b));
        System.out.println(lcm(a, b));
    }

    public static int gcd(int a, int b) {
        while (b != 0) {
            int r = a % b;
            a = b;
            b = r;
        }
        return a;
    }

    public static int lcm(int a, int b) {
        return a * b / gcd(a, b);
    }
}

[실행 결과]